PID_II
Process regulator that uses the feedback concept to regulate the
process variable according to the difference between its current value and the value of the
set point. PID achieves calculation by a method of sampling.
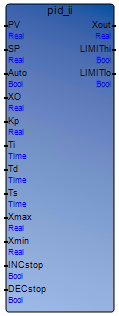
Parameter values for the PID_II function block:
Parameter | Data Type | Description | ||
|---|---|---|---|---|
PV | REAL | Process variable. Must be a REAL value. Infinity
or Not a Number (NaN) values are not supported by this input. | ||
SP | REAL | Set point. Must be a REAL value. Infinity or Not a
Number (NaN) values are not supported by this input. | ||
Auto | BOOL | Determines whether PID_II operates in AUTO or MANUAL mode. TRUE for AUTO mode FALSE for MANUAL mode | ||
XO | REAL | Adjustment value. Must be a REAL value. Infinity or Not a Number (NaN) values are
not supported by this input. In MANUAL mode, Xout = XO | ||
Kp | REAL | Proportionality constant. Must be a REAL value.
Infinity or Not a Number (NaN) values are not supported by this input. | ||
Ti | TIME | Integral time constant. Possible values range from 0ms to 23hr59m59s999ms. | ||
Td | TIME | Derivative time constant. Possible values range from 0ms to 23hr59m59s999ms. | ||
Ts | TIME | Minimum sample period. If Ts is less than the application scan time, uses the application scan time as
the effective sample interval. The maximum effective sample period is Ts plus the application scan time. Possible values range from 0ms to 23hr59m59s999ms. | ||
Xmax | REAL | Maximum value of Xout. Must be a REAL value.
Infinity or Not a Number (NaN) values are not supported by this input. | ||
Xmin | REAL | Minimum value of Xout. Must be a REAL value.
Infinity or Not a Number (NaN) values are not supported by this input. | ||
INCstop | BOOL | Increment stop. | ||
DECstop | BOOL | Decrement stop. | ||
Xout | REAL | PID_II function block output. Action required on the system to keep the regulation. Xout recalculates each time
a sample is taken. | ||
LIMIThi | BOOL | TRUE if Xout is clamped at its maximum value
(Xmax). | ||
LIMITlo | BOOL | TRUE if Xout is clamped at its minimum value
(Xmin). | ||
TIP:
Loss of precision and underflow may
occur.
When Xmax < Xmin, the function assumes that the values are reversed and
swaps the values. The Reversed error counter increments each time the function has to swap
the parameters.
When overflow occurs during execution, the stored integral and error
terms set to zero.
In AUTO mode:
- Xout sets to zero
- LIMIThi sets to FALSE
- LIMITlo sets to FALSE
In MANUAL mode:
- Xout sets to XO clamped to the range Xmin to Xmax
- LIMIThi sets to XO > Xmax
- LIMITlo sets to XO < Xmin
AUTO Mode Operation
When a new sample is made and Auto
= TRUE, calculates the output Xout:
Xout = Kp * ( E[t] + I[t]/Ti + D[t] *
Td)
where
E[t] = SP - PV (error) I[t] = I[t-1] + ( E[t] * T ) (integral term) D[t] = ( E[t] - E[t-1] ) / T (derivative term)
E[t-1] is the stored error
value, that is the value during the last sample.
I[t-1] is the stored integral term,
that is the value during the last sample.
T is the elapsed time in milliseconds since
the last sample.
On initialization, the stored integral term sets to zero, and the
action is calculated using proportional action only:
Xout = Kp * E[t]
When Ti =
0, the stored integral term sets to zero and Xout is calculated using proportional and
derivative naction only:
Xout = Kp * (E[t] + D[t] * Td)
Once Xout is calculated,
the increment stop (INCstop), decrement stop (DECstop) and the clamp (Xmax and Xmin) are
applied. When INCstop = TRUE and Xout has increased since the last sample or if DECstop =
TRUE and Xout has decreased since the last sample, Xout sets to its previous value. When
Xout > Xmax or Xout < Xmin, Xout is clamped to the range Xmin to Xmax, LIMIThi sets to
Xout > Xmax, and LIMITlo sets to Xout < Xmin.
When INCstop, DECstop, or the
clamp are active, the previous integral term is retained, that is the stored integral term
is not set to the current integral term. On initialisation, INCstop, and DECstop have no
effect.
MANUAL Mode Operation
If a new sample is made
and Auto = FALSE, the output Xout immediately follows the adjustment value (XO) clamped to
the range Xmin to Xmax. LIMIThi sets to XO > Xmax and LIMITlo sets to XO < Xmin. The
stored error term sets to (SP - PV) and the stored integral term sets to zero. The increment
and decrement stop (INCstop and DECstop) have no effect.
Example
(*FBD example with PID_II function block*)
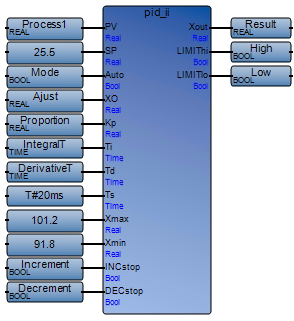
(*ST
example*)
PID_II(Process1, 25.5, Mode, Adjust, Proportion, IntegralT, DerivativeT, T#20ms, 101.2, 91.8, Increment, Decrement); Result:= PID_II.Xout; High := PID_II.LIMIThi; Low := PID_II.LIMITlo;
Provide Feedback
